Действия с корнями
В нижеприведенных формулах знаком 
обозначена
абсолютная величина корня.
1. Величина корня не изменится, если его показатель увеличить в n раз и одновременно возвести подкоренное количество в степень n:
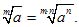
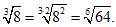
2. Величина корня не изменится, если показатель степени уменьшить в n раз и одновременно извлечь корень n-й степени из подкоренного количества:
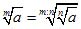
Пример 2.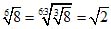
Замечание. Это свойство останется в силе и в том случае, когда число m/n не будет целым; точно так же оба вышеуказанных свойства сохранят силу и для n дробного. Но для этого нужно сначала расширить понятие степени и корня, введя дробные показатели.
3. Корень из произведения нескольких сомножителей равен произведению корней той же степени из этих сомножителей:
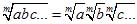
Пример 3.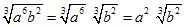
Последнее преобразование основывается на свойстве 2.
Пример 4.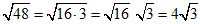
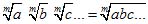
Пример 5.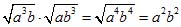
4. Корень от частного равен частному от деления корня из делимого на корень из делителя (показатели корней разумеются одинаковыми):
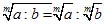
Обратно: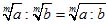
Пример 6.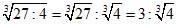
5. Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное количество:
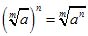
Обратно, чтобы извлечь корень из степени, достаточна, возвести в эту степень корень из основания степени:
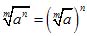
Пример 7.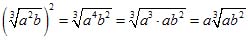
Пример 8.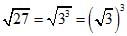
6. Уничтожение иррациональности в знаменателе или в числителе дроби. Вычисление пробных выражений, содержащих радикалы, часто облегчается, если предварительно «уничтожить иррациональность» в числителе или знаменателе, т. е. преобразовать дробь так, чтобы в числителе или знаменателе не содержались радикалы.
Пример 9. Пусть требуется вычислить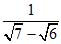
- с точностью до 0,01. Если произвести
действия в указанном порядке, то
мы имеем:
1) 
≈2,646;
2) 
≈2,449;
3) 2,646 - 2,449 = 0,197;
4) 
≈5,10.
Для получения результата нужно было выполнить четыре действия; при этом, чтобы получить верные цифры сотых, нужно было вычислить корни с
точностью до тысячных,
в противном случае и делителе дроби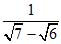получились бы только две значащие
цифры и в результате не могло бы
быть трех верных значащих цифр.
Если же предварительно помножим числитель и знаменатель данной дроби на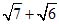 
,то
получим:
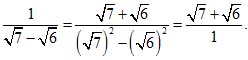
Теперь вычисление требует только трех действий, и корни можно вычислять лишь с точностью до сотых:
1) ≈2,65;
2) ≈ 2,45;
3) 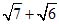≈ 5,10.
Ниже приводится еще несколько типичных примеров.
Пример 10.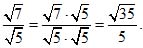
Пример 11.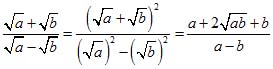
В этих примерах иррациональность уничтожалась в знаменателе. В следующих двух примерах она уничтожается в числителе.
Пример 12.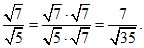
Пример 13.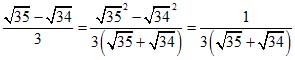
Преобразование в примере 12 явно невыгодно для вычислительных целей, так как вычисление выражения
требует деления на многозначное число; вычисление же
(см. пример 10) требует деления на целое число. Но преобразование в примере 13 выгодно, так как позволяет вычислять корни
и 
со столькими знаками, сколько их требуется иметь в результате. В исходном же выражении нужно извлекать корни с большим числом знаков
(см. пример 9). Поэтому принятое в школьной практике огульное уничтожение иррациональности в знаменателе представляет вредную схоластическую традицию.
Узнать больше
Теорема косинусов
Ловкий Карл Фридрих Гаусс
Правила округления чисел
Нахождение площади треугольника
