Алгебраическое уравнение
Алгебраические уравнения - уравнения вида Р(х1, ..., хn) = 0, где Р- многочлен от переменных х1, ..., хn. Эти переменные называют неизвестными. Упорядоченный набор чисел (a1, ..., an) удовлетворяет этому уравнению, если при замене x1 на a1, x2 на a2 и т.д. получается верное числовое равенство (например, упорядоченная тройка чисел (3, 4, 5) удовлетворяет уравнению
X2 + Y2 = Z2,
поскольку
32 + 42 = 52,
Число, удовлетворяющее алгебраическому уравнению с одним неизвестным, называют корнем этого уравнения. Множество всех наборов чисел, удовлетворяющих данному уравнению, есть множество решений этого уравнения. Два алгебраических уравнения, имеющих одно и то же множество решений, называются равносильными. Степень многочлена Р называется степенью уравнения Р(x1, ..., хn) = 0. Например, Зх - 5у + z = с - уравнение первой степени,
X2 - 3X2 + 1 = 0, - второй степени, а
X2 + Y2 = 10, - четвертой степени.
Уравнения первой степени называют также линейными.
Алгебраическое уравнение с одним неизвестным имеет конечное число корней, а множество решений алгебраического уравнения с большим числом неизвестных может представлять собой бесконечное множество определенных наборов чисел. Поэтому обычно рассматривают не отдельные алгебраические уравнения с n неизвестными, а системы уравнений и ищут наборы чисел, одновременно удовлетворяющие всем уравнениям данной системы. Совокупность всех этих наборов образует множество решений системы. Например, множество решений системы уравнений
X2 - Y2 = 8, - четвертой степени.
таково: {(3; 1), (3; - 1), ( - 3; 1), ( - 3; -1)}.
Алгебраические уравнения 1-й степени с одним неизвестным решали уже в Древнем Египте и Древнем Вавилоне. Вавилонские писцы умели решать и квадратные уравнения, а также простейшие системы линейных уравнений и уравнений 2-й степени. С помощью особых таблиц они решали и некоторые уравнения 3-й степени, например
X3 + X = a,
В Древней Греции квадратные уравнения решали с помощью геометрических построений, Греческий математик Диофант (III в.) разработал методы решения алгебраических уравнений и систем таких уравнений со многими неизвестными в рациональных числах. Например, он решил в рациональных числах уравнение
X4 - Y4 + Z4 = N4,
систему уравнений
Y3 + X2 = U2, Z2 + X2 = V3 и т.д..
Некоторые геометрические задачи: удвоение куба, трисекция угла, построение правильного семиугольника - приводят к решению кубических уравнений. По ходу решения требовалось отыскать точки пересечения конических сечений (эллипсов, парабол и гипербол). Пользуясь геометрическими методами, математики средневекового Востока исследовали решения кубических уравнений. Однако им не удалось вывести формулу для их решения. Первым крупным открытием западноевропейской математики была полученная в XVI в. формула для решения кубического уравнения. Поскольку в то время отрицательные числа еще не получили распространения, пришлось отдельно разбирать такие типы уравнений, как
X3 + PX = Q, X3 + Q = PX и т. д.
Итальянский математик С. дель-Ферро (1465-1526) решил уравнение
X3 + PX = Q,
и сообщил решение своему зятю и ученику А.М. Фиоре, который вызвал на математический турнир замечательного математика - самоучку Н. Тарталью (1499-1557). За несколько дней до турнира Тарталья нашел общий метод решения кубических уравнений и победил, быстро решив все предложенные ему 30 задач. Однако найденная Тартальей формула для решения уравнения
X3 + PX + Q = 0,
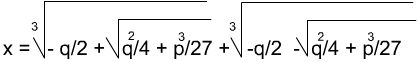
была опубликована не им, а итальянским же ученым Дж. Кардано (1501-1576), который узнал ее от Тартальи. В это же время Л. Феррари (1522-1565), ученик Кардано, нашел решение уравнения 4-й степени.
Создание алгебраической символики и обобщение понятия числа вплоть до комплексных чисел позволили в XVII-XVIII вв. исследовать общие свойства алгебраических уравнений высших степеней, а также общие свойства многочленов от одного и нескольких переменных.
Одной из самых важных задач теории алгебраических уравнений в XVII-XVIII вв. было отыскание формулы для решения уравнения 5-й степени. После бесплодных поисков многих поколений алгебраистов усилиями французского ученого XVIII в. Ж. Лагранжа (1736-1813), итальянского ученого П. Руффини (1765-1822) и норвежского математика Н. Aбеля в конце XVIII-начале XIX в. было доказано, что не существует формулы, с помощью которой можно выразить корни любого уравнения 5-й степени через коэффициенты уравнения, используя лишь арифметические операции и извлечение корней. Эти исследования были завершены работами Э. Галуа, теория которого позволяет для любого уравнения определить, выражаются ли его корни в радикалах. Еще до этого К.Ф.Гаусс решил проблему выражения в квадратных радикалах корней уравнения
Xn - 1 = 0,
к которому сводится задача о построении с помощью циркуля и линейки правильного n-угольника. В частности, невозможно с помощью этих инструментов построить правильный семиугольник, девятиугольник и т.д. - такое построение возможно лишь в случае, когда n- простое число вида
23k + 1 = 0,
или произведение различных простых чисел такого вида.
Наряду с поисками формул для решения конкретных уравнений был исследован вопрос о существовании корней у любого алгебраического уравнения. В XVIII в. французский философ и математик Ж. Д’Аламбер доказал, что любое алгебраическое уравнение ненулевой степени с комплексными коэффициентами имеет хотя бы один комплексный корень. В доказательстве Д'Аламбера были пропуски, восполненные потом Гауссом. Из этой теоремы следовало, что любой многочлен n-й степени от х разлагается в произведение n линейных множителей.
В настоящее время теория систем алгебраических уравнений превратилась в самостоятельную область математики, называемую алгебраической геометрией. В ней изучаются линии, поверхности и многообразия высших размерностей, задаваемые системами таких уравнений.
