Асимптота
Асимптота кривой - это прямая, к которой кривая приближается сколь угодно близко при удалении в бесконечность. Представьте себе мчащийся по прямолинейному шоссе автомобиль и всадника, скачущего по полю с той же скоростью, но направленной в каждый момент на автомобиль. Маршрут всадника в этом случае будет кривой линией, называемой трактрисой, для которой линия шоссе является асимптотой. Если кривая, заданная уравнением у =f(х), удаляется в бесконечность при приближении х к конечной точке а, то прямая х = а называется вертикальной асимптотой этой кривой. Такими асимптотами являются прямая х = 0 для гиперболы у = 1/х, каждая из прямых
x = kп (k = 0, ![]() 1,
1, ![]() 2, ...) для функции y = ctgx (рис. 1).
2, ...) для функции y = ctgx (рис. 1).
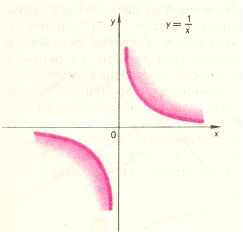
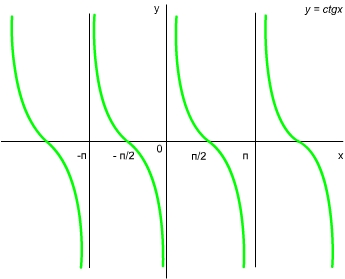
Помимо вертикальной асимптоты х = 0 гипербола у = 1/х имеет еще и горизонтальную
асимптоту у = 0, как и график функции
![]() ,
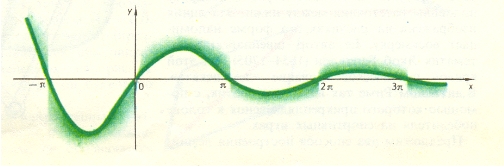
однако он, в отличие от гиперболы, пересекает свою горизонтальную асимптоту в бесконечном
множестве точек
(рис. 2).
,
однако он, в отличие от гиперболы, пересекает свою горизонтальную асимптоту в бесконечном
множестве точек
(рис. 2).
У кривой, носящей название «декартов лист» (рис. 3),
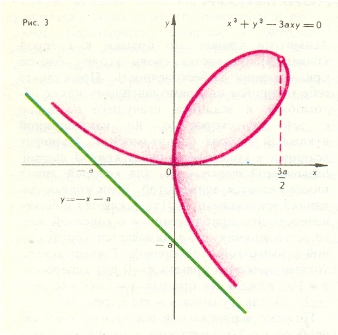
уравнение которой
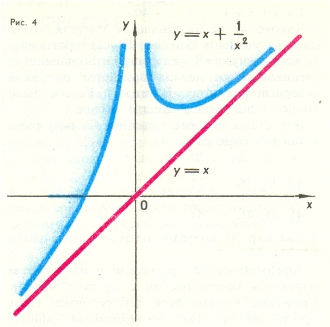
![]() , имеется наклонная асимптота, как и у кривой
, имеется наклонная асимптота, как и у кривой
![]() (рис. 4).
(рис. 4).
Коэффициенты к и b в уравнении прямой у = кх + b, являющейся наклонной асимптотой кривой у =f(х) при стремлении к плюс или минус бесконечности, находятся как пределы:
![]()
Горизонтальная асимптота является частным случаем наклонной при к = 0. Исследование асимптот позволяет более четко представить поведение графика функции, поскольку свойства функции вблизи ее асимптоты очень близки к свойствам асимптоты -линейной функции, свойства которой хорошо изучены. Систематическое использование этого свойства породило целое направление в современной математике - «асимптотические методы исследования». Таким образом, понятие, возникшее еще в Древней Греции, переживает в наше время второе рождение. Не у всякой кривой, уходящей в бесконечность, есть асимптота. Например, известная вам кривая парабола асимптот не имеет.
