Практические применения пропорций. Интерполяция
Решение многих задач связано с рассмотрением пропорциональных величин, применение правил
механизирует решение таких задач, сводя их к единой схеме, показанной ниже на примерах.
Пример 1. Суточное потребление топлива на заводе составляло до проведения рационализации 1,8 т; годовой расход на топливо
составлял 30 000 руб. После проведения рационализации суточное потребление снизилось до 1,5 т. Какую сумму расходов на
топливо нужно запланировать на год?
Безыскусственное решение задачи таково: находим
1) годовое потребление топлива до рационализации:
1,8 • 365 = 657 (т);
2) стоимость 1 т топлива: 30000:657 = 45,66 (руб.);
3) годовой расход на топливо после рационализации:
45,66 • 1,5 • 365 = 25 000 (руб.).
Гораздо быстрее и легче решить задачу, учтя, что суточное потребление топлива и годовой расход на него — величины
пропорциональные (что видно из того, что увеличение суточного потребления увеличивает в то же число раз годовой расход).
Схема решения:
1,8 т 30 000 руб.;
1,5 т х руб.;
x = (30000 * 1,5)/1,8 = 25000(руб.).
Хотя пропорциональная зависимость встречается очень часто, все же огромное число зависимостей, с которыми приходится иметь дело в практике, не подчиняется закону пропорциональности. Тем более важно отметить, что даже для таких величин схема пропорционального расчета не теряет значения. Именно, если рассматривать изменения, непропорциональных величин внутри некоторых тесных пределов, то эти изменения будут практически пропорциональны.
Поясним это примером. Сторона квадрата и era площадь не пропорциональны: например, стороне 2 м отвечает площадь 4м2, стороне 2,01 м — площадь (2,01)2 ≈ 4,0401 ≈ 4,040 (м2); стороне 1,02 — площадь 4,0804 ≈ 4,080 (м2) и так далее. Отношение сторон (например, 2,01:1), как видим, не равно отношению соответствующих площадей (4,040:1). Но отношение изменений стороны во взятых нами пределах практически равно отношению изменений площади.
Действительно, когда сторона увеличивается с 2 м до 2,01 м, ее изменение составляет 0,01 м; когда она увеличится с 2 м до 2,02 м, изменение составляет 0,02 м. Отношение изменений 0,02 : 0,01 ровно 2. Соответствующие изменения площади будут (с точностью до третьего знака) составлять: в первом случае 0,040; во, втором 0,080. Отношение изменений 0,080 : 0,040 также равно 2. Таким образом, изменение длины пропорционально изменению площади, если величины последних брать с точностью до третьего десятичного знака. Если же брать четыре десятичных знака, то обнаружится небольшое отклонение от пропорциональности. Но можно добиться, чтобы и в четвертом знаке не было никакого отклонения от пропор¬циональности; для этого нужно рассматривать изменение стороны в еще более узких пределах (скажем, не от 1 м до 1,02 м, а от 1 м до 1,002 м). Практически мы всегда учитываем только определенное количество десятичных знаков (три, четыре, редко пять). Вот почему мы можем малые изменения стороны и площади квадрата считать: величинами пропорциональными. То же явление имеет место в огромнейшем большинстве других случаев. Благодаря этому оказывается возможным по таблице, содержащей сравнительно небольшое число данных, находить и такие результаты, которых в таблице нет, как бы «читая между строк» в ней.
Пример 2. Допустим мы желаем найти
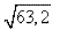 ; в таблице нет числа 63,2, но
есть 63; 64; 65 и так далее.
; в таблице нет числа 63,2, но
есть 63; 64; 65 и так далее.| Подкоренное число | Квадратный корень | Изменение квадратного корня |
| 63 64 65 |
7,937 8,000 8,062 |
0,063 0,062 |
Подсчитаем (см. третью колонку), насколько изменяется 1 величина, корня при изменении подкоренного числа на 1 , от 63 до 64 и от 64 до 65. Мы увидим, что различие в этих изменениях будет только на одну единицу третьего знака. (На самом деле это различие еще меньше: оно сказывается только в четвертом знаке, и лишь округление до трех знаков вызвало это различие.).
Если же брать только три знака, то все наши измене¬ния окажутся почти равными, т. е. в пределах между 63 и 65 изменения квадратных корней, взятые с точностью до трех десятичных знаков, пропорциональны изменениям подкоренных чисел. Поэтому мы находим
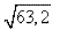 по такой схеме:
по такой схеме:| Изменение подкоренного числа | Изменение квадратного корня |
| 1 0,2 |
0,062 x |
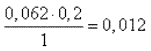
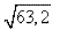 , прибавляя к
, прибавляя к
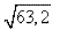 ≈ 7,949.
≈ 7,949.Если извлечем этот корень с точностью до третьего десятичного знака, то убедимся, что все знаки нашего результата правильны.
Описанный выше способ вычисления носит название интерполяции (или интерполирования). Латинское слово «интерполяция» в переводе означает «вставка внутрь». В математике интерполяцией называется всякий способ, с помощью которого по таблице, содержащей некоторые числовые данные, можно найти промежуточные результаты, которые непосредственно не даны в таблице. Рассмотренный нами простейший способ интерполяций называется линейной интерполяцией.
Интерполяция широко применяется при пользовании таблицами самого разнообразного содержания.
