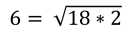Отношение и пропорция
Частное от деления одного числа на другое называется также их отношением. Термин "отношение" применялся прежде только в тех случаях, когда требовалось выразить одну величину в долях другой, однородной с первой, например одну длину в долях другой, одну площадь в долях другой площади и т. д., что выполняется с помощью деления.
Отсюда понятно, почему появился особый термин "отношение": раньше его смысл был иной, чем термина "деление", который относили к делению некоторой именованной величины на отвлеченное число. Сейчас этого различия не делают; говорят, например, об отношении неоднородных величин, скажем веса тела к его объёму и т. д. Когда речь идет об отношении однородных величин, его часто выражают в процентах.
Пример №1
В библиотеке 10 000 книг; из них 8000 на русском языке; каково отношение числа русских книг к общему их числу? 8000:10 000 = 0,8. Искомое отношение есть 0,8 или 80 %.
Делимое называют предыдущим членом отношения, делитель - последующим. В нашем примере 8000 - предыдущий член, 10 000 - последующий.
Два равных отношения образуют пропорцию. Так, если в одной библиотеке 10000 книг, из них 8000 на русском языке, в, другой библиотеке - 12 000 книг, из них 9600 на русском языке, то отношение числа русских книг к общему числу книг в обеих библиотеках одинаково:
8000:10000 = 0,8;
9600:12 000 = 0,8.
Мы имеем здесь пропорцию, которая записывается так:
8000 : 10 000 = 9600 : 12 000.
Говорят: "8000 относится к 10 000 так, как 9600 к 12 000". 8000 и 12 000 - крайние члены; 10000, и 9600 - средние члены пропорции.
Произведение средних членов пропорции равно произведению крайних. В нашем примере
8000 * 12 000= 96 000 000;
10 000 * 9600 = 96 000 000.
Один из крайних членов пропорции равен произведению средних членов, деленному на другой крайний. Точно так же один из средних членов равен произведению крайних, деленному на другой средний.
Если
a:b =c:d,
то

и т. д. Так в нашем примере

Этим свойством постоянно пользуются для вычисления неизвестного члена пропорции, когда три остальных члена известны.
Пример №2
12 : х = 6 : 5 (х обозначает неизвестное число).

Пропорция, в которой средние члены равны, называется непрерывной; например, 18:6 = 6:2. Средний член непрерывной пропорции есть среднее, геометрическое крайних членов; в нашем примере