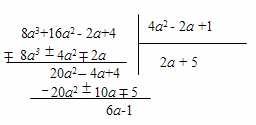Деление сумм и многочленов
Частное от деления суммы двух или нескольким выражений на какое-либо выражение равно сумме частных, полученных от деления каждого слагаемого на взятое выражение:
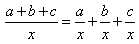
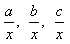бывает возможно упростить.
Пример. 
.
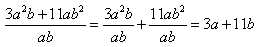Если а, b, с — одночлены, а х — многочлен, т. е. если выполняется деление многочлена на многочлен, то частное, вообще
говоря, нельзя представить в виде многочлена (подобно тому как частное от деления целого числа на целое не всегда можно
представить в виде целого числа). Иначе говоря, не всегда можно найти такой многочлен, который, будучи умножен на
многочлен, стоящий в делителе, дал бы многочлен, стоящий в делимом.
Пример. Частное (a2 + x2)/(a + x) нельзя представить в виде многочлена;
частное (a2 - x2)/(a + x) можно
представить в виде многочлена: (a2 - x2)/(a + x) = (a -x).
Деление многочлена на многочлен в общем случае можно выполнять с остатком, подобно тому как это делается при делении целых
чисел. Необходимо, однако, установить, что такое деление многочленов с остатком. Если мы делим целое положительное число,
например 35, на целое положительное число, например 4, то получаем 8 и 3 в остатке. Числа 8 и 3 обладают тем свойством, что
4 • 8 + 3 = 35, т. е. если р - делимое, q - делитель, m — частное, а n —остаток, то mq+ n = р. Но этого недостаточно для
полного определения частного и остатка; так, в нашем примере (р = 35, q = 4) таким же свойством обладают также числа
m = 6, n = 11; m = 4; n = 19. Нужно еще добавить, что число n должно быть меньше числа q. Это добавление нельзя буквально
перенести на случай деления многочленов, ибо при одних значениях букв одно и то же выражение может быть больше, а при
других - меньше, чем другое выражение. Упомянутое добавление должно быть видоизменено. В каждом из многочленов одна
какая-нибудь из входящих в его члены букв принимается за главную; наивысшая степень этой буквы называется степенью
многочлена. Тогда деление с остатком определяется так.
Разделить многочлен Р на многочлен Q - значит найти многочлены М (частное) и N (ocmamoк), удовлетворяющие двум
требованиям:
1) должно соблюдаться равенство MQ+N = Р и
2) степень многочлена N должна быть ниже степени многочлена Q.
Замечание. Остаток N может вовсе не содержать главной буквы; тогда говорят, что N имеет нулевую степень.
Многочлены М и N, удовлетворяющие этим требованиям, всегда можно найти и притом единственным образом при данном выборе
главной буквы. Однако они могут быть иными, если изменить выбор главной буквы. Процесс нахождения частного М и остатка N
аналогичен процессу деления (с остатком) многозначного числа на многозначное. Роль цифр высшего и низшего разрядов играют
члены, содержащие главную букву в высшей и низшей степенях. Перед делением члены делимого и делителя располагаются в
порядке убывания степеней главной буквы.
Запись деления:
