Возведение комплексного числа в любую действительную степень

Возведение в дробную степень действительного числа определенно в §61. Но там рассматриваются только, действительные значения степени. Здесь мы нуждаемся в более общем определении. Оно дается следующей формулой:

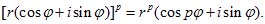   (C)
Здесь р - любое действительное число, a r^p означает положительное число, представляющее р-ю степень модуля r. Формула (С) совпадает с формулой (A) (§46), когда, p - целое число, и с (В) (§47), когда р есть дробь 1/n . Если р есть дробь m/n, то в силу (С), (А) и (В) 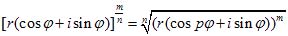,    (D)
чтo согласуется с обычным определением дробной степени.
Дробная степень всякого комплексного (в том числе и действительного) числа имеет п различных между собой значений (п - знаменатель дроби). Формула (С) распространяется и на случай, иррациональности показателя р. В последнем случае р-я степень всякого числа имеет бесчисленное множество значений.
Пример 1. Возвести число -16 в степень 3/4 . Имеем:
p = 3/4, r =16; φ = 180° + 360° k. Модуль степени (-16^3/4) согласно (С) равен 16^3/4 =8. Аргумент степени равен 3/4 * (180° + 360°k) = 135° + 270°. Полагая k = 0, 1, 2, 3 (остальные целые значения k новых результатов не дадут), имеем следующие четыре значения степени:
z1 = 8(cos 135° + isin135°) = ;
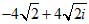z2 = 8 [cos (135° + 270°) + isin (135° + 270°)] =
= 8 (cos 45° + isin 45°) = ;
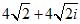z3 = 8 [cos (135° + 2•270°) + isin (135° + 2•270°)] =
= 8 [cos (- 45°) + isin (- 45°)] = ;
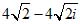z4 = 8 [cos (135° + 3 • 270°) + isin (135° + 3•270°)] =
= 8 [cos (- 135°) + isin (- 135°)] = _ .
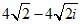Эти значения изображены точками В1, В2, B3, B4 (фиг. 19).
Пример 2. Возвести число 1 в степень . Здесь p = , r =1, φ = 360° k. Согласно (С) имеем:


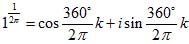
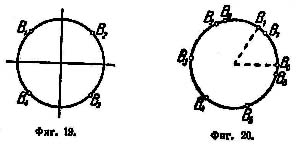
На фиг. 20 показаны точки В0, В1, B2, B3, …, изображающие те значения степени, которые получаются при k = 0, 1, 2, 3,... Все они лежат на окружности радиуса 1. Никакие пары этих точек не совпадают друг с другом. В самом деле, каждый из углов В0ОВ1, В1ОВ2 и т. д. равен радиану, т. е. каждая из дуг В0В1, В1В2 и т. д. имеет длину равную радиусу. Если, бы некоторая точка В1 совпадала с В0, то оказалось бы, что окружность, обойденная s раз (s - некоторое целое число), содержала бы l радиусов. Tогда однократно обойденная окружность имела бы длину, в точности равную L/S радиусов.
Но окружность несоизмерима с радиусом. Значит, ни одна пара точек В0, В1, … не совпадает. Чем больше точек мы берем, тем плотнее покрывается ИМИ окружность. Около любой ее точки скопляются бесконечное множество точек В. И все же повсюду на окружности остаются такие точки, куда не попадает ни одна из точек В. Такова, например, точка, диаметрально противоположная точке В0, или любая вершина какого-нибудь правильного многоугольника, для которого В0 есть одна из вершин.
Замечание. Можно определить степень комплексного числа и для комплексного показателя степени. Она тоже имеет бесчисленное множество значений, но соответствующие точки в общем случае не скопляются, а лежат врозь друг от друга.