Геометрический смысл деления комплексных чисел

Деление есть действие, обратное умножению. Поэтому (cм. предыдущий параграф) при делении комплексных чисел их модули делятся (модуль делимого на модуль делителя), а аргументы вычитаются (аргумент делителя из аргумента делимого) т. е.

r( cosφ + i sinφ ) : r'( cosφ' + isinφ' ) = r/r' * [cos ( φ - φ' ) + isin ( φ - φ')]. (1)
Пример 1.
2(cos30 + isin30):6(cos45 + isin45) = 1/3 * [cos(-15) + isin(-15)]
Пример 2.
- 4: (cos45° + isin45°) = 4 (cos180° + isin180°): (cos45° + isin45°) = ( cos135° + isin135°). См. пример 2 предыдущего параграфа.
В алгебраической форме:

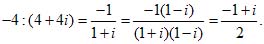
Пример 3. Разделить 1 на комплексное число r(cosφ + isinφ). Запишем делимое в виде 1(cos0° + isin0°). Согласно формуле (1) частное будет
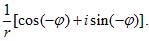
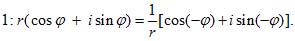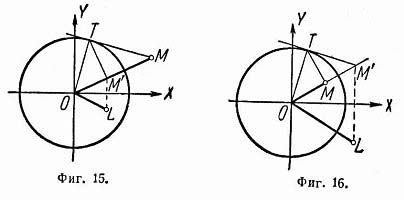
(2)
Геометрическое построение: опишем окружность радиуса 1 с центром в О. Пусть > 1,т.е. точка М (фиг. 15), изображающая делитель, лежит вне окружности. Проведем касательную МТ, из точки Т проведем перпендикуляр ТM' к OM. Точка L, симметричная с М' относительно оси абсциcc, изображает частное. Действительно, |OL| = |ОМ'|, а из прямоугольного треугольника ОТМ, в котором ТМ' – высота, |ОТ|2 = |OМ| • |OМ'|, т.е. 1 = r |OМ'| или |ОМ'| = 1/r. Аргументы же векторов ОМ и OL, очевидно, равны по величине и противоположны по знаку.
Для случая |r| < 1 построение показано на фиг. 16.
Из формул (2) следует, что от деления 1 на комплексное число с модулем r = 1 получается комплексное число, сопряженное с делителем.

Пример 4.
2 [cos (- 30°) + isin ( - 30°)] : 6 [cos ( - 45) + isin ( - 45°)] = 1/3 * (cos 15°+ isin 15°).
Сравнив с примером 1, видим, что от замены делимого и делителя сопряженными числами частное заменилось сопряженным числом. Формула (1) показывает, что это свойство - общее.