Система уравнений второй степени с двумя неизвестными
Наиболее общий вид уравнения 2-й степени с двумя неизвестными есть
ах2 + bху + су2 + dx + ey + f = 0,
где а, b, с, d, е, f — данные числа или выражения, содержащие известные
величины. Одно уравнение 2-й степени с двумя неизвестными имеет бесчисленное множество решений.
Система двух уравнений с двумя неизвестными, из которых одно - квадратное, а другое - 1-й степени, можно решить способом подстановки.
Выражение одного неизвестного через другое находится из уравнения 1-й степени. Подставив это выражение в уравнение второй степени, получим уравнение с одним неизвестным.
В общем случае оно будет квадратным (см. пример 1). Но может оказаться, что члены второй степени взаимно уничтожатся, и тогда мы будем иметь уравнение первой
степени (см. пример 2).
Пример 1. х
2 - 3xy + 4у
2 - 6х + 2у = 0, х - 2у = 3. Из второго уравнения находим х = 3 + 2у.
Подставляя это выражение в первое уравнение, имеем:
(3 +2у)
2 - 3(3 + 2y)у + 4y
2- 6(3 + 2у) + 2у = 0.
Решаем это уравнение:
9 + 12y + 4y
2 -9y - 6y
2 +4y
2 -18 -12y +2y = 0;
2y
2 -7y -9 = 0;
y =
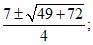
y
1 = 9/2 ; y
2 = -1.
Найденные значения y
1 = 9/2 ; y
2 = -1 подставляем в выражение x = 3 +2y; получаем x
1 = 12, x
2 = 1.
Пример 2. x
2 – y
2 = 1; x + y = 2.
Из второго уравнения находим у = 2 - х. Подставляя это выражение в первое уравнение, получим х
2 - (2 - х)
2 = 1. После приведения подобных членов члены
второй степени взаимно уничтожаются, и мы получаем - 4 + 4x = 1, откуда x = 5/4. Подставляя это значение в выражение у = 2 - х, находим y = 3/4.
Систему двух квадратных уравнений с двумя неизвестными можно решать так: если одно из уравнений не содержит члена ах
2 (или члена су
2), то применяем
способ подстановки,
выражая из этого уравнения х (или у) через у (или х); если же оба уравнения содержат члены вида ах
2 и су
2, то предварительно применяем способ сложения или вычитания,
чтобы получить уравнение, не содержащее члена ах
2 или су
2. После этого пользуемся способом подстановки. После исключения получается уравнение с одним неизвестным, имеющее,
вообще говоря, 4-ю степень. К квадратному уравнению оно сводится лишь в исключительных случаях, но эти случаи встречаются довольно часто при решении геометрических задач.
Пример 3.
x
2 + xy + 2y
2 = 74, 2x
2 + 2xy + y
2 = 73.
Оба уравнения содержат как члены с x
2, так и члены с y
2. Поэтому сначала применим способ сложения или вычитания, чтобы получить уравнение, не содержащее,
скажем y
2.
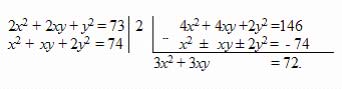
Из последнего уравнения находим выражение y через x:
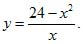
Это выражение подставляем в одно из данных уравнений, например в первое, получаем:
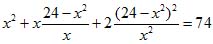
Упрощения дают:
x4 +24x2 – x4 +1152 – 96x2 +2x4 = 74x2;
2x4 -146x2 +1152 = 0;
x4 – 73x2 +576 = 0.
Получилось биквадратное уравнение.
Положив x2 = z, приводим его к уравнению z2 – 73z + 576 = 0.
Решая последнее находим:
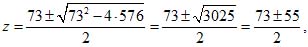 z1 = 64; z2 = 9.
z1 = 64; z2 = 9.
Первое решение дает x
1 = 8; x
2 = - 8; второе x
3 = 3; x
4 = -3. Подставляя значения x
1; x
2; x
3; x
4 в выражение
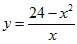
, получаем соответствующие им значения y:
y1 = - 5; y2 = + 5; y3 = +5; y4 = - 5.
Для решения систем уравнений второй степени часто можно с успехом использовать искусственные приемы решения, позволяющие с успехом получить результат быстрее и изящнее.
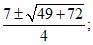 y1 = 9/2 ; y2 = -1.
Найденные значения y1 = 9/2 ; y2 = -1 подставляем в выражение x = 3 +2y; получаем x1 = 12, x2 = 1.
Пример 2. x2 – y2 = 1; x + y = 2.
Из второго уравнения находим у = 2 - х. Подставляя это выражение в первое уравнение, получим х2 - (2 - х)2 = 1. После приведения подобных членов члены
второй степени взаимно уничтожаются, и мы получаем - 4 + 4x = 1, откуда x = 5/4. Подставляя это значение в выражение у = 2 - х, находим y = 3/4.
Систему двух квадратных уравнений с двумя неизвестными можно решать так: если одно из уравнений не содержит члена ах2 (или члена су2), то применяем
способ подстановки,
выражая из этого уравнения х (или у) через у (или х); если же оба уравнения содержат члены вида ах2 и су2, то предварительно применяем способ сложения или вычитания,
чтобы получить уравнение, не содержащее члена ах2 или су2. После этого пользуемся способом подстановки. После исключения получается уравнение с одним неизвестным, имеющее,
вообще говоря, 4-ю степень. К квадратному уравнению оно сводится лишь в исключительных случаях, но эти случаи встречаются довольно часто при решении геометрических задач.
Пример 3.
x2 + xy + 2y2 = 74, 2x2 + 2xy + y2 = 73.
Оба уравнения содержат как члены с x2, так и члены с y2. Поэтому сначала применим способ сложения или вычитания, чтобы получить уравнение, не содержащее,
скажем y2.
y1 = 9/2 ; y2 = -1.
Найденные значения y1 = 9/2 ; y2 = -1 подставляем в выражение x = 3 +2y; получаем x1 = 12, x2 = 1.
Пример 2. x2 – y2 = 1; x + y = 2.
Из второго уравнения находим у = 2 - х. Подставляя это выражение в первое уравнение, получим х2 - (2 - х)2 = 1. После приведения подобных членов члены
второй степени взаимно уничтожаются, и мы получаем - 4 + 4x = 1, откуда x = 5/4. Подставляя это значение в выражение у = 2 - х, находим y = 3/4.
Систему двух квадратных уравнений с двумя неизвестными можно решать так: если одно из уравнений не содержит члена ах2 (или члена су2), то применяем
способ подстановки,
выражая из этого уравнения х (или у) через у (или х); если же оба уравнения содержат члены вида ах2 и су2, то предварительно применяем способ сложения или вычитания,
чтобы получить уравнение, не содержащее члена ах2 или су2. После этого пользуемся способом подстановки. После исключения получается уравнение с одним неизвестным, имеющее,
вообще говоря, 4-ю степень. К квадратному уравнению оно сводится лишь в исключительных случаях, но эти случаи встречаются довольно часто при решении геометрических задач.
Пример 3.
x2 + xy + 2y2 = 74, 2x2 + 2xy + y2 = 73.
Оба уравнения содержат как члены с x2, так и члены с y2. Поэтому сначала применим способ сложения или вычитания, чтобы получить уравнение, не содержащее,
скажем y2.
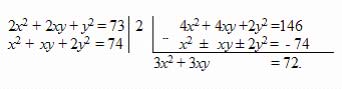
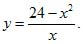
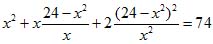
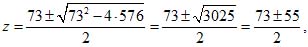 z1 = 64; z2 = 9.
z1 = 64; z2 = 9.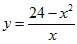 , получаем соответствующие им значения y:
, получаем соответствующие им значения y:
