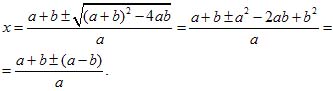Решение квадратного уравнения
Чтобы найти решение приведенного квадратного уравнения
x2 + px +q = 0,
достаточно перенести свободный член в правую часть и к обеим частям равенства прибавить ![]() .
Тогда левая часть станет полным квадратом, и мы получим равносильное уравнение
.
Тогда левая часть станет полным квадратом, и мы получим равносильное уравнение
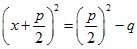 .
.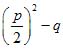 - вместо m. Находим:
- вместо m. Находим:
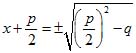 .
Отсюда
.
Отсюда
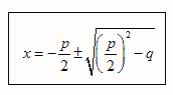 (1)
(1)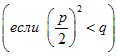 .
Может оказаться, что оба корня квадратного уравнения равны между
собой
.
Может оказаться, что оба корня квадратного уравнения равны между
собой 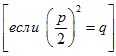 .
Формулу (1) особенно удобно употреблять в том случае, когда p – целое четное число.
Пример 1.
x2 – 12x - 28 = 0; здесь p = - 12; q = -28.
.
Формулу (1) особенно удобно употреблять в том случае, когда p – целое четное число.
Пример 1.
x2 – 12x - 28 = 0; здесь p = - 12; q = -28.
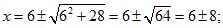 x1 = 6 + 8 = 14;
x2 = 6 – 8 = - 2.
Пример 2. x2+12x+10=0;
x1 = 6 + 8 = 14;
x2 = 6 – 8 = - 2.
Пример 2. x2+12x+10=0;
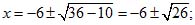
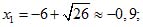
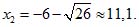 Пример 3. x2-2mx+m2-n2 = 0;
Пример 3. x2-2mx+m2-n2 = 0;
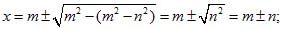 x1=m+n; x2=m-n.
Замечание. В примере 2 оба корня - действительные отрицательные числа, но иррациональные. Квадратные корни, получающиеся при решении квадратных уравнений, можно
извлекать с помощью вычисления или находить по таблицам. К сожалению, в большинстве задачников упражнения на квадратные уравнения нарочито составляются так, чтобы
корни извлекались точно. На практике же подобные случаи встречаются очень редко. Поэтому мы настоятельно рекомендуем учащимся избавиться от той боязни иррациональных решений,
которая создается вследствие упомянутой особенности задачников.
Когда р не является целым четным числом, при решении приведенного квадратного уравнения предпочтительно пользоваться нижеприведенной более общей формулой (3), полагая в ней а = 1
(см. ниже, пример 5).
Неприведённое полное квадратное уравнение
x1=m+n; x2=m-n.
Замечание. В примере 2 оба корня - действительные отрицательные числа, но иррациональные. Квадратные корни, получающиеся при решении квадратных уравнений, можно
извлекать с помощью вычисления или находить по таблицам. К сожалению, в большинстве задачников упражнения на квадратные уравнения нарочито составляются так, чтобы
корни извлекались точно. На практике же подобные случаи встречаются очень редко. Поэтому мы настоятельно рекомендуем учащимся избавиться от той боязни иррациональных решений,
которая создается вследствие упомянутой особенности задачников.
Когда р не является целым четным числом, при решении приведенного квадратного уравнения предпочтительно пользоваться нижеприведенной более общей формулой (3), полагая в ней а = 1
(см. ниже, пример 5).
Неприведённое полное квадратное уравнение
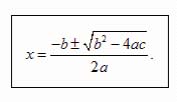 (3)
(3)
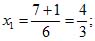
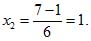 Пример 5. x2+7x+12 = 0
(a = 1, b = 7, с = 12).
Пример 5. x2+7x+12 = 0
(a = 1, b = 7, с = 12).
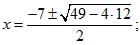 x1 = - 3; x2 = - 4.
Пример 6. 0,60x2 +3,2 x - 8,4 = 0
x1 = - 3; x2 = - 4.
Пример 6. 0,60x2 +3,2 x - 8,4 = 0
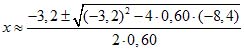 ;
;
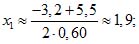
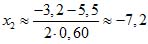 .
В примере 6, как явствует из написания 0,60х2 (а не 0,6х2) коэффициенты предполагаются приближенными числами. Поэтому и действия, указываемые формулой, рекомендуется выполнять
сокращенным способом, изложенным в разделе арифметика, 32—43; во всяком случае нужно обязательно учесть, что согласно правилам, изложенным в указанных параграфах, в результате
можно иметь только
две точные значащие цифры. Заметим, что наши результаты верны с точностью до 0,1, но это отнюдь не означает, что, подставив их в левую часть данного уравнения, мы получим число,
равное нулю с точностью до 0,1. Напротив, подставив в левую часть, например, значение х = 1,9, мы получим:
0,60 • 1,92 + 3,2 • 1,9 - 8,4 ≈ - 0,2.
Но если значение х увеличить на 0,1 и взять х = 2,0 то получим:
0,60 • 2,02 + 3,2 • 2,0 - 8,4 ≈ 0,4.
Таким образом, при х = 1,9 левая часть была отрицательна; при x = 2,0 она уже положительна. Значит, она равна нулю каком-то значении х, лежащем между 1,9 и 2,0. Следовательно,
беря х = 1,9, мы ошибаемся не больше чем на 0,1. Это и имеется в виду, когда говорят, что корень равен 1,9 с точностью до 0,1.
Если b – четное число, то лучше представить общую формулу в виде
.
В примере 6, как явствует из написания 0,60х2 (а не 0,6х2) коэффициенты предполагаются приближенными числами. Поэтому и действия, указываемые формулой, рекомендуется выполнять
сокращенным способом, изложенным в разделе арифметика, 32—43; во всяком случае нужно обязательно учесть, что согласно правилам, изложенным в указанных параграфах, в результате
можно иметь только
две точные значащие цифры. Заметим, что наши результаты верны с точностью до 0,1, но это отнюдь не означает, что, подставив их в левую часть данного уравнения, мы получим число,
равное нулю с точностью до 0,1. Напротив, подставив в левую часть, например, значение х = 1,9, мы получим:
0,60 • 1,92 + 3,2 • 1,9 - 8,4 ≈ - 0,2.
Но если значение х увеличить на 0,1 и взять х = 2,0 то получим:
0,60 • 2,02 + 3,2 • 2,0 - 8,4 ≈ 0,4.
Таким образом, при х = 1,9 левая часть была отрицательна; при x = 2,0 она уже положительна. Значит, она равна нулю каком-то значении х, лежащем между 1,9 и 2,0. Следовательно,
беря х = 1,9, мы ошибаемся не больше чем на 0,1. Это и имеется в виду, когда говорят, что корень равен 1,9 с точностью до 0,1.
Если b – четное число, то лучше представить общую формулу в виде
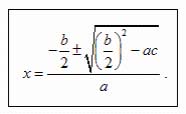
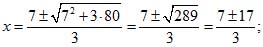 x1 = 8; x2 = .
Этой же формулой удобно пользоваться, когда коэффициенты a, b, c – буквенные выражения.
Пример 8. ax2 -2(a+b)x +4b = 0;
x1 = 8; x2 = .
Этой же формулой удобно пользоваться, когда коэффициенты a, b, c – буквенные выражения.
Пример 8. ax2 -2(a+b)x +4b = 0;